In de klas: 'Wat is de 'duration' van een obligatie?

Bijdragen

Deze blog komt tot stand dankzij bijdragen van de analisten van KBC Asset Management, KBC Securities, KBC Market Research en de economen, contentmanagers van Bolero en aandelenstrategen van KBC Groep:

Allison Mandra, Andrea Gabellone, Benjamin Wolff, Bérangère Bivort, Bernard Keppenne, Cora Vandamme, Dieter Guffens, Dirk Thiels, Ellen Van Tongelen, Guy Sips, Hans Dewachter, Jacob Mekhael, Jens Meersman, Jo Elsocht, Johan Van Gompel, Joren De Mesmaeker, Joris Franck, Kurt Ruts, Kristof Samoy, Laurent Convent, Lieven Noppe, Lynn Hautekeete, Mathias Janssens, Mathias Van der Jeugt, Marion Geubel,Michiel Declercq, Peter Wuyts, Philippe Delfosse, Sharad Kumar Surendran Palani, Siegfried Top, Thibault Leneeuw, Thomas Couvreur, Thomas Vranken, Tom Noyens, Tom Simonts, Wim Hoste en Wim Lewi.

Disclaimer

Deze publicatie van KBC Bank N.V. (Bolero) wordt uitsluitend ter informatie verstrekt en is niet bedoeld als een specifiek en persoonlijk beleggingsadvies, een aanbieding of een uitnodiging tot een aanbieding, om de hierin vermelde financiële producten te kopen of te verkopen, noch onafhankelijk onderzoek op beleggingsgebied.

De dienstverlening die Bolero verschaft, is niet op beleggingsadvies gebaseerd. Bolero is het orderuitvoeringsplatform van KBC Bank N.V. waarmee transacties in ‘niet-complexe’ financiële producten (in de zin van MiFID II) doorgaan op basis van ‘loutere uitvoering’ (“execution only”). Bolero voert geen ‘passendheidstoetsing’ uit bij transacties in niet-complexe financiële producten. De belegger die van deze dienstverlening gebruik maakt, beschikt dus niet over de bescherming van de toepasselijke gedragsregels. Transacties in ‘complexe’ financiële producten (in de zin van MiFID II) kunnen pas uitgevoerd worden na een succesvolle passendheidstoetsing. Transacties via Bolero gebeuren altijd op initiatief van de belegger.

Bij het uitvoeren en/of doorgeven van transacties van beleggers houdt Bolero geen rekening met de daarmee verband houdende fiscale, juridische of boekhoudkundige aspecten van deze transacties, verstrekt zij geen advies met betrekking tot dergelijke aspecten en kan zij daarvoor derhalve niet aansprakelijk worden gesteld.

Beleggen in financiële producten houdt risico’s in. Beleggers moeten in staat zijn om het economische risico van een belegging te dragen en het belegde kapitaal geheel of gedeeltelijk te verliezen.

Deze blog bevat publicaties van KBC Securities NV (https://research.kbcsecurities.com/portal/portal.html#!/disclosures), KBC Asset Management NV (https://www.kbc.be/particulieren/nl/juridische-info/documentatie-beleggen.html#aandelen) en KBC Economics (https://www.kbc.com/nl/economics.html). Voor de externe bronnen raadpleegt Bolero verschillende nieuwssites. De bijdragen worden geselecteerd op basis van recente, concrete gebeurtenissen en publicaties. De redactie wordt verzorgd door Tom Simonts (KBC Securities) en door Jo Elsocht, Joren De Mesmaeker, Jens Meersman, Ellen Van Tongelen en Philippe Delfosse (marketing team Bolero, KBC Bank NV). KBC Bank staat onder toezicht van de FSMA.

wo. 28 feb 2024

12:00

Wat is duration ? Duration is de (gewogen) gemiddelde looptijd van een obligatie. De duration is een maatstaf voor het effect dat een renteverandering heeft op de koers van een obligatie of een portefeuille van obligaties.

In een vorig artikel beschreven we dat een obligatiekoers stijgt (daalt) wanneer de marktrente daalt (stijgt). Het begrip duration geeft weer in welke mate de obligatiekoers stijgt of daalt. Obligaties met een lange looptijd zijn rentegevoeliger dan kortlopende obligaties.

Vandaar dat fondsbeheerders van obligatiefondsen de duration van de obligatieportefeuille verlengen als de rente stijgt. Ze kopen bijgevolg obligaties met een langere looptijd. Wanneer de rente nadien daalt, stijgt de obligatiekoers. Het fonds profiteert dan maximaal van een rentedaling.

Berekening

We nemen als voorbeeld een obligatie op 2 jaar met een couponrente van 5% en een actuarieel rendement (YTM = yield to maturity) van 5%. Het inlegbedrag is 1.000 euro.

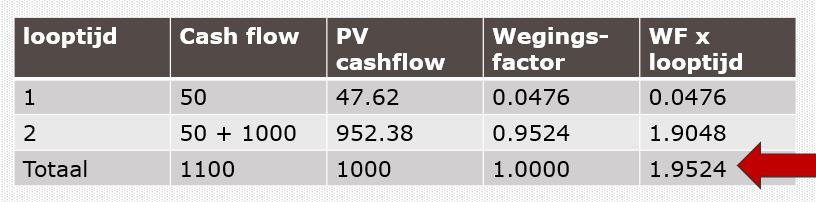
Na het eerste jaar ontvangt de belegger 50 euro opbrengst (5% coupon op 1.000 euro). In jaar 2 ontvangt de belegger opnieuw 50 euro rente maar krijgt de belegger ook het initiële bedrag (1.000 euro) terug. Dit vinden we terug onder de kolom ‘cash flow’ (kolom 2).

We berekenen de huidige waarde van de toekomstige inkomsten (kolom 3) Dat doen we door de opbrengst te delen door 1 + YTM. In ons voorbeeld, voor het eerste jaar:

PV Cashflow = ------------- = 47,62 (1)

(1 + 0,05)

PV Cashflow = present value (huidige waarde) van de opbrengst

We berekenen dit eveneens voor het tweede jaar :

50 + 1000

PV Cashflow = ------------------ = 952,38 (2)

(1 + 0,05)²

We tellen (1) en (2) samen en bekomen 1000.

De wegingsfactor (d.i. het gewicht van het eerste jaar, resp. het tweede jaar in de berekening) is:

voor het eerste jaar (1)/1000 = 47,62/1000 = 0,0476
voor het tweede jaar (2)/1000 = 952,38/1000=0,9524.

Tenslotte vermenigvuldigen we de weggingsfactor met de looptijd:

voor het eerste jaar 0,0476 * 1 = 0,0476
voor het tweede jaar 0,9524 x 2 = 1,9048

Opgeteld geeft dat 0,0476 + 1,9048 = 1,9524.

Om te komen tot de duratie van de obligatie rest ons enkel nog de som te delen door (1+YTM).

1,9524/(1+0.05) = 1,8594

De duratie van de obligatie (ook wel modified duration genoemd) = 1,8594.

Dit betekent dat wanneer de marktrente stijgt met 1%, de obligatiekoers zal dalen met 1,8594%. Wanneer de marktrente daalt met 1%, zal de obligatiekoers stijgen met 1,8594%.

Naar overzicht